SUPERPOSITION
Since ac circuits are linear, the superposition theorem applies to ac circuits the same way it applies to dc circuits. It becomes important if the circuit has sources operating at different frequencies. In this case, since the impedances depend on frequency, we must have a different frequency domain circuit for each frequency. The total response must be obtained by adding the individual responses in the time domain. It is incorrect to try to add responses in the phasor or frequency domain. Because the exponential factor e^jwt is implicit in sinusoidal analysis, and that factor would change for every angular frequency w. It would therefor not make sense to add responses at different frequencies in the phasor domain. Thus, when a circuit has sources operating at different frequencies, one must add the responses due to the individual frequencies in the time domain.
Example we gather from the book:
Use The superposition theorem to find Io in the circuit in the figure below:
So First we let
Io=I'o + I''o
Where I'o and I''o are due to the voltage and current sources, respectively. To find I'o consider the circuit in figure a. If we let Z be the parallel combination of -j2 and 8+j10, then
Z=-j2(8+j10)/-2j+8+j10=0.25-j2.25
And current I'o is
I'o=j20/4-j2+Z
=J20/4.25-j4.25
or I'o= -2.353 + j2.353
To get I''o, consider the circuit in figure b. For mesh 1,
(8+j8)I1-j10I3+j2I2=0
For mesh 2,
(4-j4)I2+J2I1+J2I3=0
For mesh 3.
I3=5
From equations of mesh 2 and mesh 3
(4-j4)I2+j2I1+j10=0 =>eq 1
Expressing I1 in terms of I2 gives
I1=(2+j2)I2-5 =>eq 2
Substituting equation of mesh 3 and equation 2 into equation of mesh 1 we get
(8+j8)[(2+j2)I2-5]-j50+j2I2=0
or I2=90-40/34 =2.647-j1.176
Current I''o is obtained as
I''o=-I2=-2.647+j1.176
From the quation I'o=-2.353+j2.353 and I''o=-I2 we write
Io=I'o+I''o=-5+j3.529
=6.12angle144.78 A










 . Give the expression of this current as a function of time
. Give the expression of this current as a function of time  .
. ,
,  ,
,  ,
,  . As cosine function
. As cosine function  reaches maximum when
reaches maximum when  (or
(or  ), the phase angle
), the phase angle  should satisfy
should satisfy  where
where  and
and  , i.e.,
, i.e.,


 , same as above.
, same as above.


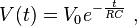
 is called the RC time constant and is given by
is called the RC time constant and is given by









